FUNGSI KUADRAT 

1. Pengertian Fungsi Kuadrat
Fungsi kuadrat yaitu suatu fungsi yang pengkat variabel tertingginya adalah dua.
Bentuk umum:

y = ax² + bx + c = 0, a≠0 dan a,b,c elemen RBaca juga : Materi Lengkap Persamaan Kuadrat || Kumpulan Soal Lengkap Persamaan Kuadrat

2. Grafik Fungsi KuadratGrafik fungsi kuadrat berupa parabola dengan posisi parabola ditentukan oleh nilai a.a. Jika a > 0 maka parabola terbuka ke atas

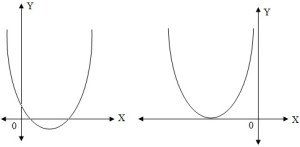
b. Jika a < 0 maka parabola terbuka ke bawah

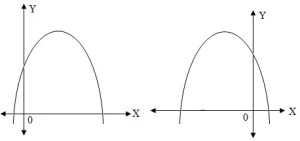
3. Titik Potong terhadap Sumbu-sumbu KoordinatTitik potong terhadap sumbu-sumbu koordinat, terdiri atas dua macam, yakni:
a. Titik potong terhadap sumbu X
Agar grafik fungsi kuadrat y = ax² + bx + c = 0 memotong sumbu X maka nilai y haruslah sama dengan 0
y = 0 <=> ax² + bx + c = 0
                (x – x1)(x – x2) = 0
Koordinat titik potongnya adalah (x1, 0) dan (x2, 0)

b. Titik potong pada sumbu Y 
Agar grafik fungsi kuadrat y = ax² + bx + c = 0 memotong sumbu Y maka nilai x haruslah sama dengan 0
x = 0 <=> y = a(0)² + b(0) + c = c

Koordinat titik potongnya adalah (0 , c)

Baca: Contoh Soal Lengkap Fungsi Kuadrat >>

4. Titik Puncak/Titik Balik dan Sumbu Simetri
Bentuk y = ax² + bx + c dapat ditulis menjadi y = a(x + b/2a)² + [(b² – 4ac)/-4a]
x disebut sumbu simetri
y disebut nilai ekstrim
=> Jika a > 0 maka y.eks = y.min
=> Jika a < 0 maka y.eks = y.max
      Titik puncak parabola : [(-b/2a) , (b² – 4ac)/-4a]
=> Jika a > 0 maka titik puncak adalah titik balik minimum dan parabola terbuka ke atas.
=> Jika a < 0 maka titik puncak adalah titik balik maksimum dan parabola terbuka ke bawah.

5. Kegunaan Diskriminan pada Fungsi Kuadrat
a. Mengetahui hubungan parabola dengan sumbu X
   1) Jika D > 0 maka parabola memotong sumbu X pada dua titik
   2) Jika D = 0 maka parabola menyinggung sumbu X
   3) Jika D < 0 maka parabola tidak menyinggung ataupun memotong sumbu X
   Perhatika grafik fungsi kuadrat y = ax² + bx + c

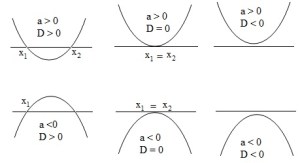
b. Mengetahui hubungan parabola dengan garis
Untuk menentukan apakah suatu garis itu memotong atau tidak memotong parabola, maka dapat dilakukan dengan cara mensubtitusikan garis ke parabola, dan hasilnya seperti di bawah ini.
1) Jika D > 0 maka garis memotong parabola di titik
2) Jika D = 0 maka garis menyinggung parabola (berpotongan di satu titik)
3) Jika D < 0 maka garis tidak menyinggung ataupun memotong parabola

6. Menentukan Persamaan Kurva dari Fungsi Kuadrat
Untuk menentukan persamaan kurva jika grafik fungsi kuadratnya diketahui dapat dilakukan dengan cara berikut.
a. Jika diketahui titik puncak = (xp , yp), gunakan rumus:
    y = a(x – xp)² + yp 
b. Jika diketahui titik potong dengan sumbu X yakni (x1 , 0) dan (x2,0) gunakan rumus: y = a(x – x1)(x – x2)
c. Jika yang diketahui selai titik pada poin a dan b, maka gunakan rumus: y= ax² + bx +c.